Advanced AI/ML Methodologies
The study of complex physical phenomena and high-dimensional scientific datasets presents significant challenges across engineering and scientific disciplines. Effectively predicting system behavior, optimizing designs, and understanding underlying mechanisms often requires advanced computational tools that can handle vast amounts of data, propagate uncertainties, and operate efficiently. Traditional simulation methods can be computationally prohibitive, while empirical approaches may lack generalizability or fail to capture intricate interdependencies. This necessitates the development of sophisticated artificial intelligence and machine learning methodologies to accelerate discovery and enhance decision-making.
A core focus in this area involves advancing techniques for surrogate modeling, uncertainty quantification, and interpretability. Surrogate models, particularly reduced-order models, aim to replace expensive high-fidelity simulations with faster, data-driven approximations. Integrating probabilistic frameworks is crucial for quantifying the inherent uncertainties in complex systems and making robust predictions. Furthermore, with the increasing complexity of AI models, ensuring interpretability is paramount, especially in scientific contexts where understanding the “why” behind predictions is as important as the predictions themselves. Addressing these challenges enables more rapid exploration of design spaces, real-time control, and a deeper scientific understanding of systems ranging from turbulent fluid flows to material stress fields.
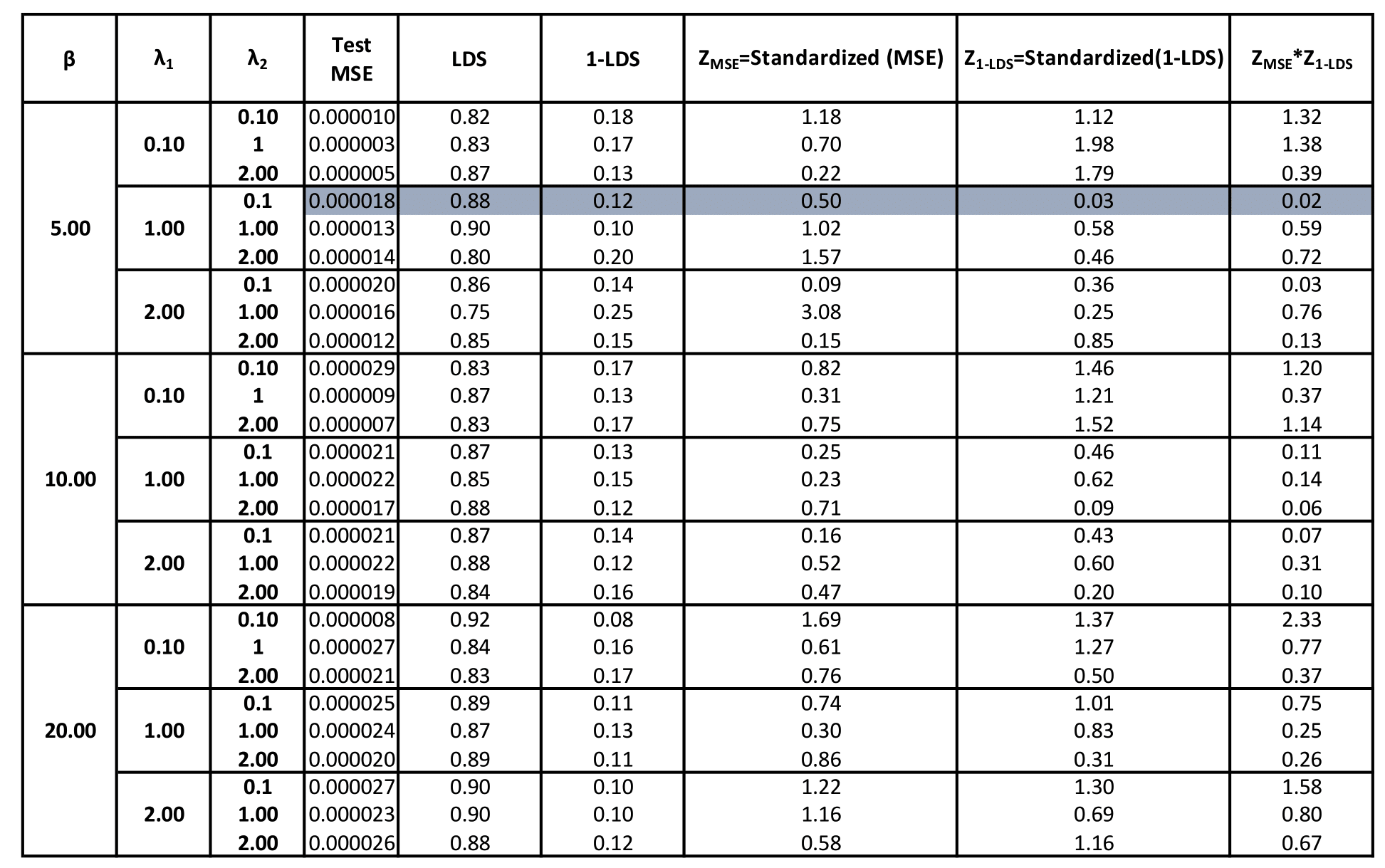
My research systematically addresses these critical challenges by developing and applying advanced AI/ML methodologies. I have focused on enhancing interpretability in generative modeling by designing frameworks that achieve statistically disentangled latent spaces, guided by known generative factors in scientific datasets. This approach provides clearer insights into the underlying mechanisms driving data generation. Furthermore, I have developed and applied robust probabilistic modeling and automated machine learning frameworks, specifically tailored for analyzing high-dimensional stress fields, allowing for a comprehensive understanding of complex mechanical behaviors while quantifying associated uncertainties.
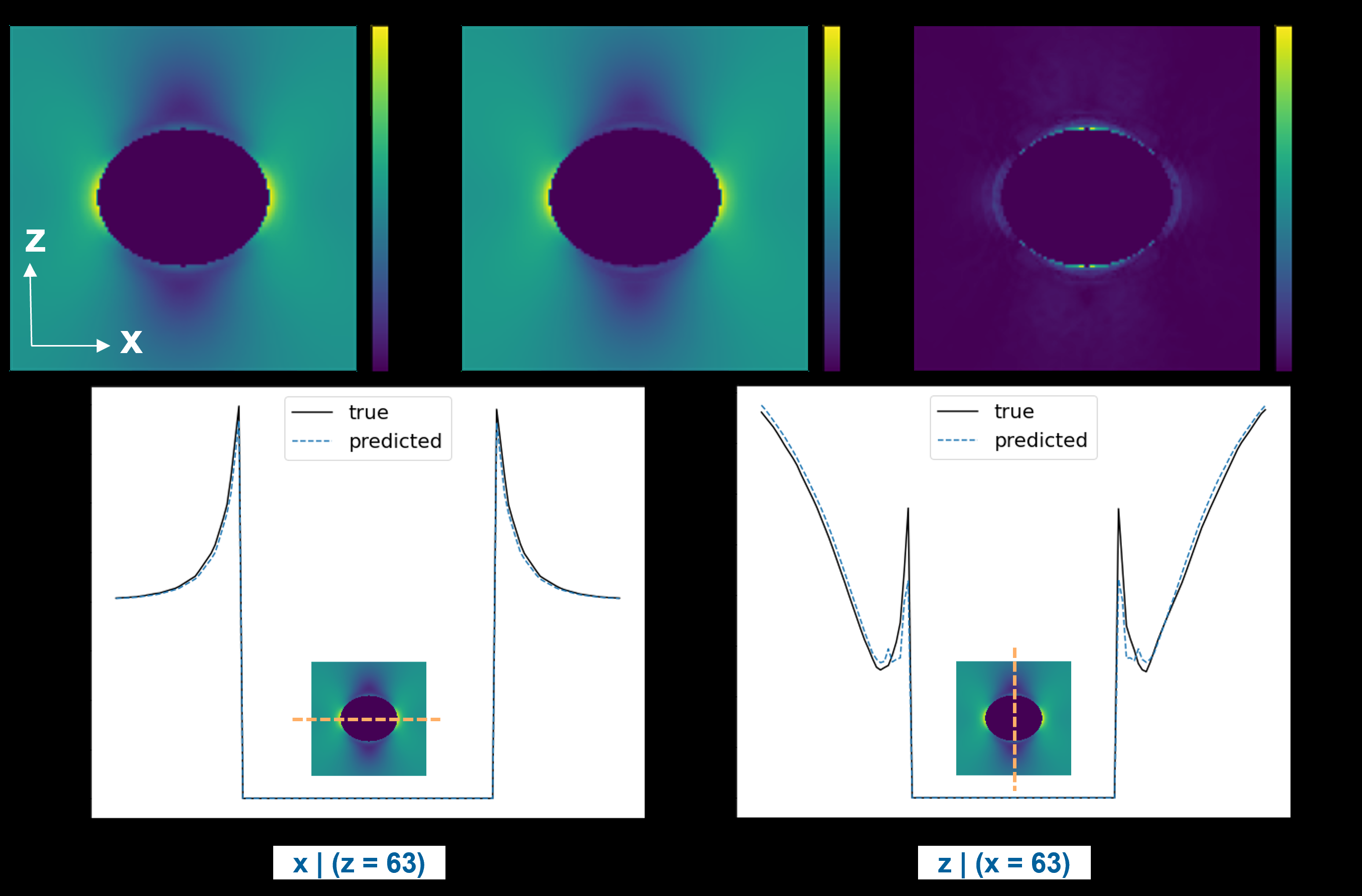
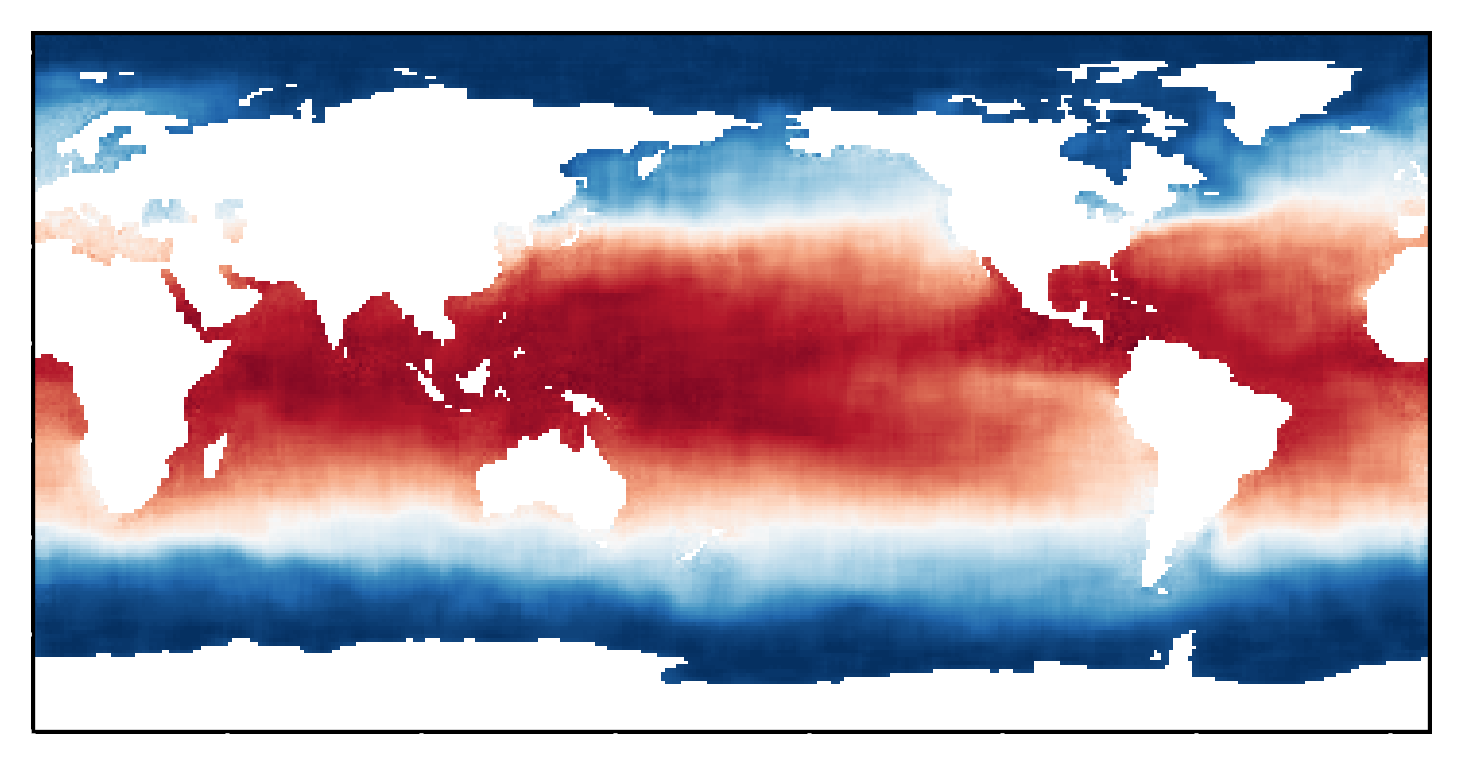
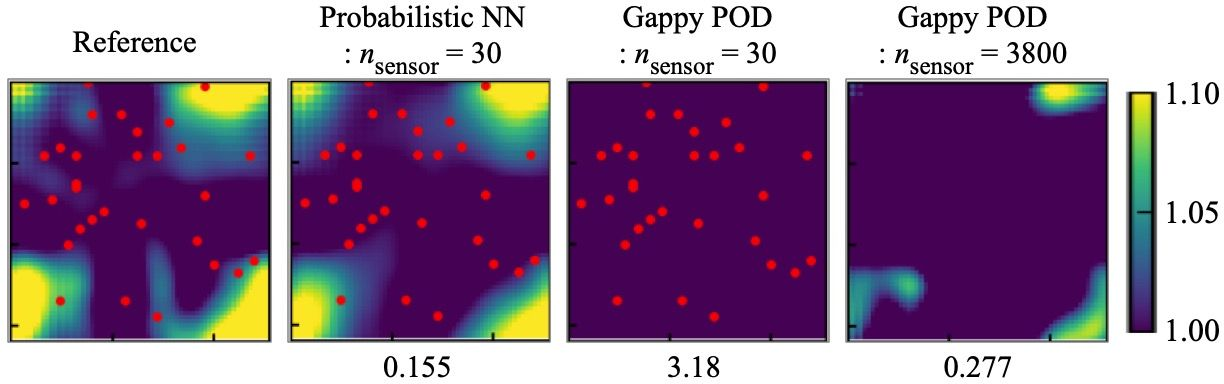
My work extends to developing efficient and reliable surrogate models for computationally intensive simulations, particularly in fluid dynamics. I have engineered probabilistic neural networks to create reduced-order surrogates for fluid flows, providing both accurate predictions and a quantification of predictive uncertainty. Complementing this, I have explored latent-space time evolution for non-intrusive reduced-order models using Gaussian process emulation, which offers a powerful way to evolve system dynamics efficiently in a compressed representation. Additionally, I have pioneered methods for global field reconstruction from sparse sensor data, utilizing deep learning techniques assisted by Voronoi tessellation to accurately recover complete spatial fields from limited observations. Through these contributions, my goal is to enable more efficient analysis, prediction, and understanding of complex scientific and engineering systems.