Scientific Emulation, Inference & Uncertainty Quantification
Scientific emulation, inference, and uncertainty quantification (UQ) are critical pillars in modern computational science, addressing the challenges posed by increasingly complex and computationally intensive physical models. Across diverse domains, from astrophysics and cosmology to fluid dynamics and high energy physics, researchers frequently encounter models that are too slow to run for extensive parameter exploration, statistical inference, or real-time prediction. This necessitates the development of sophisticated surrogate models, or emulators, capable of accurately mimicking high-fidelity simulations at a fraction of the computational cost.
Beyond mere speed, a crucial aspect of scientific prediction is understanding the reliability of results. Uncertainty quantification provides the rigorous framework to characterize and propagate uncertainties arising from model parameters, observational noise, and inherent model limitations. This involves developing methods to not only produce predictions but also to quantify the confidence in those predictions, often through probabilistic frameworks. Integrating machine learning and advanced statistical techniques into this process allows for the creation of interpretable and robust predictive tools that accelerate scientific discovery and enhance the trustworthiness of data-driven insights. Reduced-order modeling further contributes by simplifying high-dimensional systems, making complex simulations more tractable and amenable to emulation.
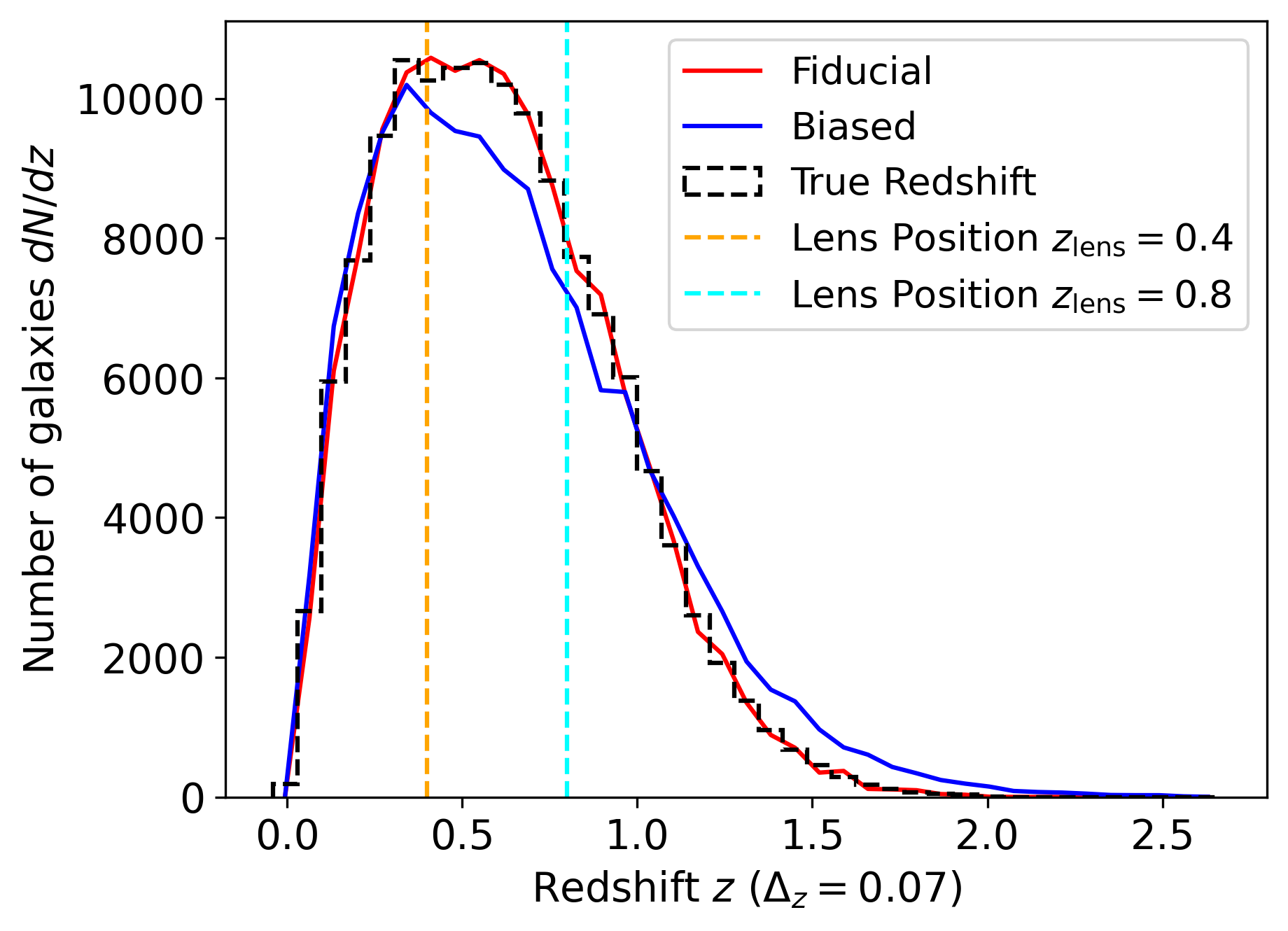
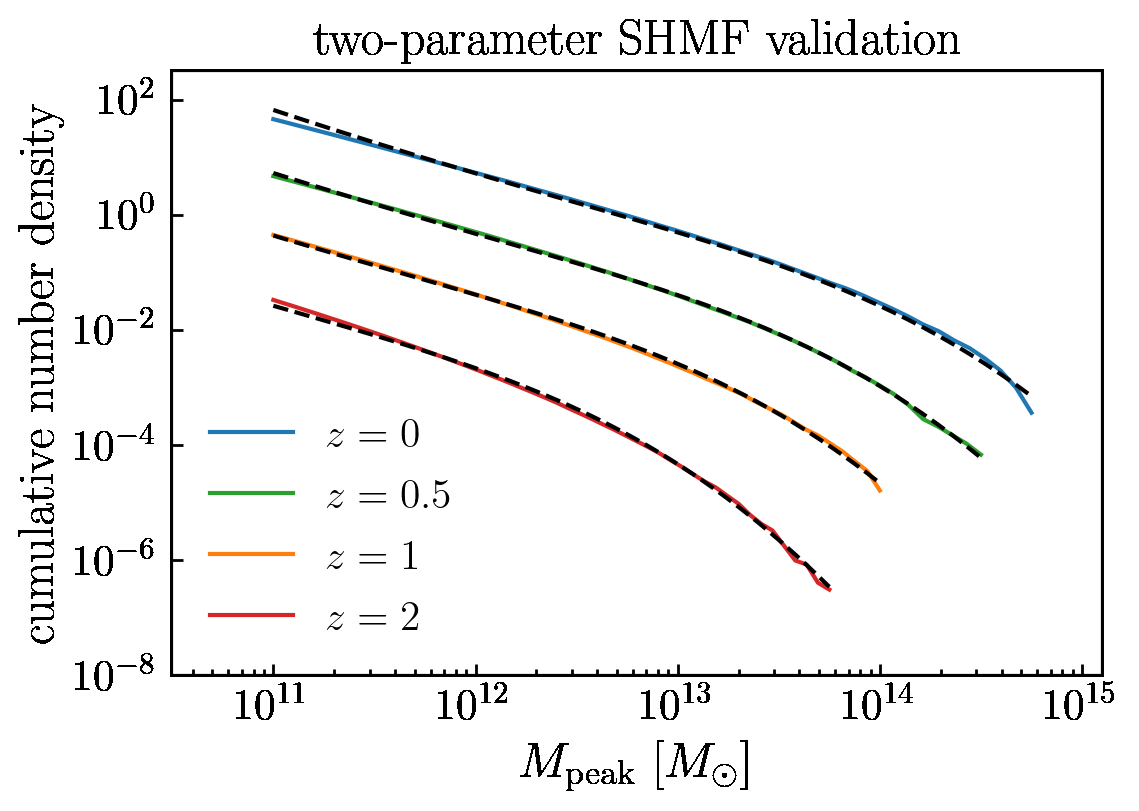
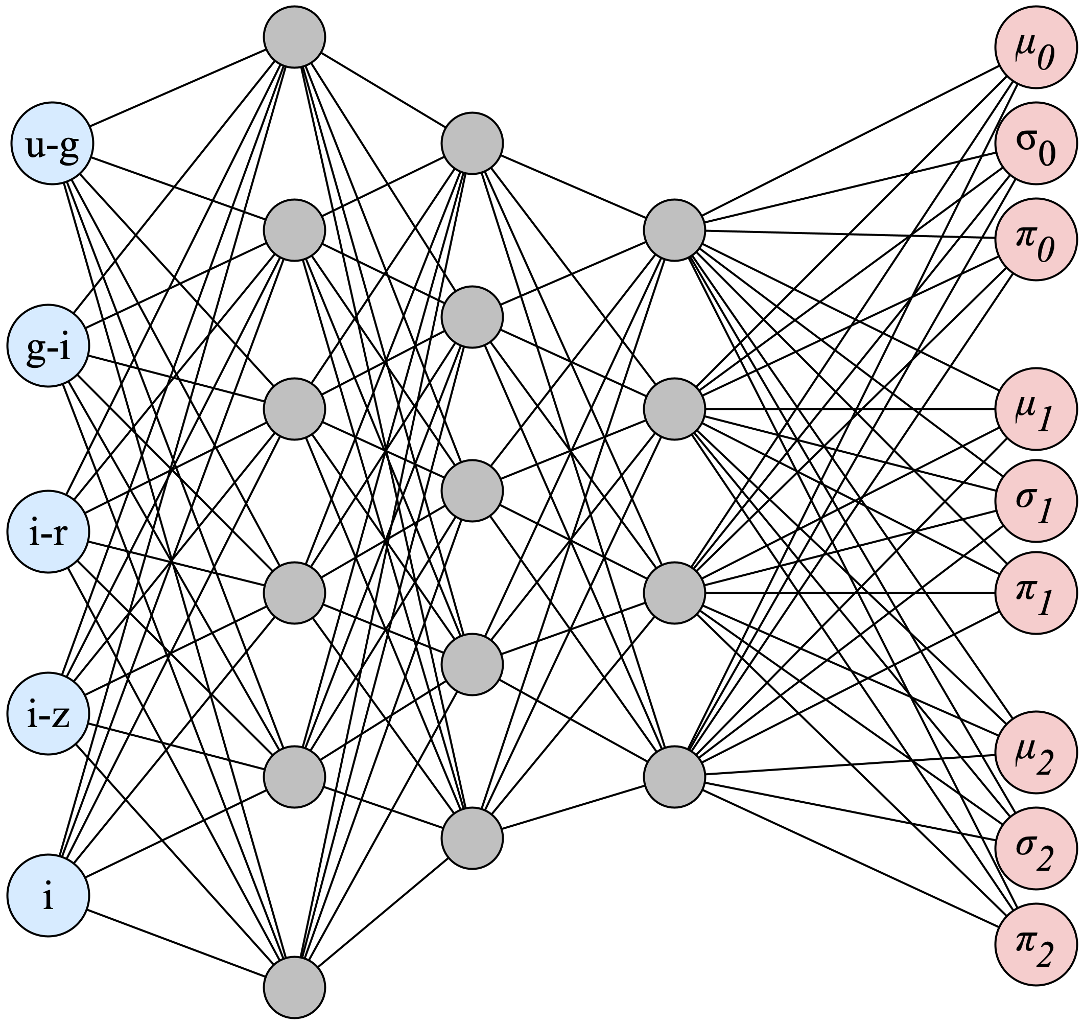
My research extensively contributes to this vital field by developing novel methodologies and applications for scientific emulation, inference, and uncertainty quantification. I have focused on leveraging advanced machine learning techniques, particularly neural networks and Gaussian processes, to build efficient and reliable surrogate models for complex scientific phenomena. For instance, I have developed SHAMNet for differentiable predictions of large scale structure, enabling more robust cosmological inference, and created a Matter Power Spectrum Emulator specifically for f(R) Modified Gravity Cosmologies, drastically accelerating predictions in alternative gravity theories. In astrophysics, I designed SYTH-Z, a machine learning approach for generating synthetic spectra and performing probabilistic redshift estimation, alongside methods for reducing model error in weak lensing cluster mass estimation through optimized galaxy selection.
A significant portion of my work is dedicated to integrating robust uncertainty quantification into these emulators and models. I have developed probabilistic neural network (PNN) based reduced-order surrogates for fluid flows, also extending these PNNs for effective data recovery and incorporating Gaussian process emulation for latent-space time evolution in non-intrusive reduced-order models. This allows for both efficient simulation and a clear understanding of predictive uncertainties in dynamic systems. Furthermore, I have focused on making AI models more transparent, exemplified by my work on interpretable uncertainty quantification in AI for High Energy Physics. Collectively, these contributions provide faster, more reliable, and transparent predictive tools, empowering deeper scientific inquiry and enabling breakthroughs in computationally challenging domains.